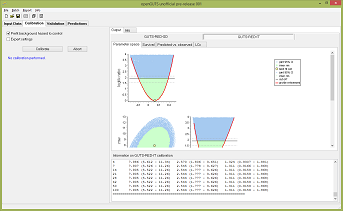
OpenGUTS is a user-friendly software to perform analyses with GUTS: the General Unified Threshold model for Survival. GUTS is the leading toxicokinetic-toxicodynamic framework for the endpoint survival (and other non-reversible all-or-nothing effects). 

This site hosts the software itself, as a standalone Windows executable, with manuals and background documentation. Since openGUTS is (as the name implies) open source, also the source files can be obtained here. Additionally, you can download the Matlab version, which served as the blueprint for the standalone version. The Matlab version has basically the same functionality, and can be easily adapted or extended to perform customised analyses. Finally, we provide (links to) further information on openGUTS and GUTS. The main features of the software are:

1. Open and free: the software is open source and freely downloadable. The fully-functional Matlab version that served as the prototype is also available.
2. User-friendly: fit models and derive confidence intervals without requiring user interaction (e.g., no need for starting values).
3. Robust: always find the global optimum and relevant intervals, even for awkward data sets.
4. Flexible: allow time-varying exposure, missing data, simultaneous fitting on multiple data sets, etc.
5. Efficient: rapid screening of exposure profiles (e.g., FOCUS output) by batch processing.
6. Supportive: the software follows the workflow as laid down in the 2018 EFSA opinion on TKTD models.

Survival is a relevant endpoint for many questions related to the effects of chemicals in the environment. Making sense of mortality, as a process over time, requires mechanism-based models, known as toxicokinetic-toxicodynamic (TKTD) models. All published TKTD models for survival can now be viewed as members of an over-arching framework: GUTS.

Click on the book cover or here to view the e-book.

Preface

1 Introduction

2 Description of GUTS

3 Mathematical treatment

4 Case study: dieldrin in guppies

5 Case study: propiconazole in amphipods

6 Use cases

7 Ring test

8 Model evaluation

9 Outlook

Bibliography

Glossary

Appendices

The General Unified Threshold model for Survival (GUTS) integrates previously published toxicokinetic-toxicodynamic models and estimates survival with explicitly defined assumptions. Importantly, GUTS accounts for time-variable exposure to the stressor. We performed three studies to test the ability of GUTS to predict survival of aquatic organisms across different pesticide exposure patterns, time scales and species. Firstly, using synthetic data, we identified experimental data requirements which allow for the estimation of all parameters of the GUTS proper model. Secondly, we assessed how well GUTS, calibrated with short-term survival data of Gammarus pulex exposed to four pesticides, can forecast effects of longer-term pulsed exposures. Thirdly, we tested the ability of GUTS to estimate 14-day median effect concentrations of malathion for a range of species and use these estimates to build species sensitivity distributions for different exposure patterns. We find that GUTS adequately predicts survival across exposure patterns that vary over time. When toxicity is assessed for time-variable concentrations species may differ in their responses depending on the exposure profile. This can result in different species sensitivity rankings and safe levels. The interplay of exposure pattern and species sensitivity deserves systematic investigation in order to better understand how organisms respond to stress, including humans. (open access, Nature Scientific Reports)

Why do some individuals survive after exposure to chemicals while others die? Either, the tolerance threshold is distributed among the individuals in a population, and its exceedance leads to certain death, or all individuals share the same threshold above which death occurs stochastically. The previously published General Unified Threshold model of Survival (GUTS) established a mathematical relationship between the two assumptions. According to this model stochastic death would result in systematically faster compensation and damage repair mechanisms than individual tolerance. Thus, we face a circular conclusion dilemma because inference about the death mechanism is inherently linked to the speed of damage recovery. We provide empirical evidence that the stochastic death model consistently infers much faster toxicodynamic recovery than the individual tolerance model. Survival data can be explained by either, slower damage recovery and a wider individual tolerance distribution, or faster damage recovery paired with a narrow tolerance distribution. The toxicodynamic model parameters exhibited meaningful patterns in chemical space, which is why we suggest toxicodynamic model parameters as novel phenotypic anchors for in vitro to in vivo toxicity extrapolation. GUTS appears to be a promising refinement of traditional survival curve analysis and dose response models. (Published in Environmental Science & Technology, open access)

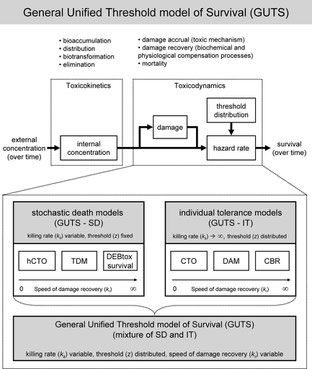
Toxicokinetic-toxicodynamic models (TKTD models) simulate the time-course of processes leading to toxic effects on organisms. Even for an apparently simple endpoint as survival, a large number of very different TKTD approaches exist. These differ in their underlying hypotheses and assumptions, although often the assumptions are not explicitly stated. Thus, our first objective was to illuminate the underlying assumptions (individual tolerance or stochastic death, speed of toxicodynamic damage recovery, threshold distribution) of various existing modeling approaches for survival and show how they relate to each other (e.g., critical body residue, critical target occupation, damage assessment, DEBtox survival, threshold damage). Our second objective was to develop a general unified threshold model for survival (GUTS), from which a large range of existing models can be derived as special cases. Specific assumptions to arrive at these special cases are made and explained. Finally, we illustrate how special cases of GUTS can be fitted to survival data. We envision that GUTS will help increase the application of TKTD models in ecotoxicological research as well as environmental risk assessment of chemicals. It unifies a wide range of previously unrelated approaches, clarifies their underlying assumptions, and facilitates further improvement in the modeling of survival under chemical stress. (link at journal) or (download here)

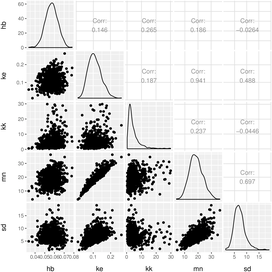
The General Unified Threshold model of Survival (GUTS) provides a consistent mathematical framework for survival analysis. However, the calibration of GUTS models is computationally challenging. We present a novel algorithm and its fast implementation in our R package, GUTS, that help to overcome these challenges. We show a step-by-step application example consisting of model calibration and uncertainty estimation as well as making probabilistic predictions and validating the model with new data. Using self-defined wrapper functions, we show how to produce informative text printouts and plots without effort, for the inexperienced as well as the advanced user. The complete ready-to-run script is available as supplemental material. We expect that our software facilitates novel re-analysis of existing survival data as well as asking new research questions in a wide range of sciences. In particular the ability to quickly quantify stressor thresholds in conjunction with dynamic compensating processes, and their uncertainty, is an improvement that complements current survival analysis methods. PLoS Comput Biol 12(6): e1004978.